QUELQUES SUJETS MAPLE
![]()
RETOUR A LA PAGE PRINCIPALE - FICHIERS TELECHARGEABLES
![]()
Maple est actuellement enseigné dans
pratiquement tous les premiers cycles des enseignements scientifiques (DEUG, classes
préparatoires aux grandes écoles, ... ) et bien entendu, de très nombreux
ouvrages - cours et exercices - sont consacrés à cet enseignement.
Je tiens simplement à faire figurer ici les
sujets qui m'ont paru, à mon humble avis, les plus attrayants et
motivants. J'utilise à dessein ces deux dernières épithètes pour bien
souligner le critère essentiel que j'ai retenu dans mes choix, à savoir le
point de vue de l'étudiant ! En effet, quoiqu'on en dise, un TP sur la méthode
de Newton pour la recherche des solutions d'une équation, reste rébarbatif s'il
ne s'accompagne pas d'une carotte quelconque, que ce soit un paradoxe numérique
lié à certaines approximations instables ou l'apparition d'une image fractale
comme j'en donne un exemple ci-dessous. C'est donc en ce sens que j'ai effectué
ma sélection.
Je ne manquerai pas de faire figurer
dans cette page tous les exemples qui me parviendront et qui iront dans cette
direction. Contactez-moi ici ou là !
Je fournis donc ici, les énoncés sous forme
de fichier Word (ou .dvi) et les corrigés en Maple (le tout en fichier.zip),
pour les sujets dont je suis l'auteur.
J'indique les références bibliographiques ou les liens Internet pour ceux qui
ne sont pas de mon cru.
Enfin <nouveau>, je
mets à disposition un polycopié sur l’utilisation
de Maple, en tant que logiciel de calcul formel, de calculs mathématiques et de
calcul numérique. Ce document fait référence à la version 7 de Maple,
maintenant un peu ancienne, mais est aisément modifiable et adaptable aux
versions actuelles. Chacun peut donc utiliser ce texte, à fin d’enseignement
par exemple, et l’actualiser à loisir, pourvu qu’il fasse apparaître une
mention du type « adapté du
polycopié de P. Vollat, professeur de mathématiques à l’Ecole Nationale des
Travaux Publics de l’Etat ».
![]()
REMARQUE SUPPLEMENTAIRE
Maple est un logiciel à usages multiples :
1.
C'est d'abord (?)
un logiciel de calcul formel, qui permet donc de manipuler des
" formes normales " (rationnels, polynômes à
coefficients rationnels, ... ) et d’effectuer avec elles de gros calculs, menés
à terme de façon exacte (au sens de l’unicité de l’identification à 0).
Il existe bien
entendu des logiciels de calcul formel plus performants que Maple, mais ils
sont alors dédiés à des domaines ciblés (théorie des nombres, groupes, idéaux,
... )
2.
Maple est aussi
un logiciel de " calculs mathématiques " surpuissant, de
par sa souplesse d’utilisation d’une part et le volume impressionnant de ses
bibliothèques d’autre part. Sont ainsi abordables, tous les calculs
d’intégration, de développements asymptotiques ou en séries diverses, de
résolutions d’équations différentielles, ...
Les calculs sont
alors menés de façon formelle ou numérique.
3.
Maple dispose
enfin d’un langage de programmation efficace et élégant.
Il est alors
possible de réaliser l’implantation en Maple de n’importe quel algorithme, soit
pour un résultat direct lors de travaux scientifiques, soit pour la mise en
place de tests préalables aux développements d’applications les plus diverses
(C++, tableurs, ... ).
L’aspect numéro 2 est actuellement largement
(et presque exclusivement) développé dans les Classes Préparatoires.
L’accent sera plutôt mis ici sur les points 1
et 3 développés ci dessus.
Quoiqu’il en soit, il s'agit toujours de faire
prendre conscience de la multiplicité de Maple, qui doit devenir un outil
efficace dans de multiples circonstances : recherches de solutions
numériques ou formelles de problèmes mathématisés (mis en équations),
simulations de contraintes, développements de projets, analyse de données, ...
Voici
donc quelques références ou/et quelques fichiers téléchargeables :
![]() Ainsi que <nouveau>
le polycopié sur l’utilisation de Maple : PolyMaple.zip
Ainsi que <nouveau>
le polycopié sur l’utilisation de Maple : PolyMaple.zip
![]()
![]() Bassins d'attraction du système dynamique discret associé à
l'itération de Newton pour la recherche des racines de x3-1 =
0
Bassins d'attraction du système dynamique discret associé à
l'itération de Newton pour la recherche des racines de x3-1 =
0
![]() Dans
ce TP, on commence classiquement par mettre en place l'itération de newton pour
la recherche des racines de f(x) = 0 (f vérifiant certaines bonnes
conditions) : un+1 = un - f(un)/f
'(un) et on réalise des visualisations graphiques sur
quelques exemples.
Dans
ce TP, on commence classiquement par mettre en place l'itération de newton pour
la recherche des racines de f(x) = 0 (f vérifiant certaines bonnes
conditions) : un+1 = un - f(un)/f
'(un) et on réalise des visualisations graphiques sur
quelques exemples.
![]() Comme
je le signalais plus haut, cet algorithme n'a en soi rien de palpitant !
Comme
je le signalais plus haut, cet algorithme n'a en soi rien de palpitant !
Aussi, admet-on ensuite (à moins qu'on ne le démontre !) la généralisation du
procédé à certaines fonctions d'une variable complexe satisfaisant à certaines
hypothèses de régularité, comme c'est le cas de f(x) = x3-1
.
Mais l'équation x3-1 = 0 ayant 3 racines complexes, on se
doute que la suite de Newton convergera vers l'une ou l'autre d'entre elles
suivant la valeur de u0 .
On parcourt alors une région du plan complexe en la quadrillant de pas
en pas et en lançant en chaque point l'itération Newton. On colore le
point en rouge, bleu ou vert suivant que la suite de Newton converge vers l'une
ou l'autre racine.
L'étudiant de première année découvre alors un résultat auquel il ne
s'attendait pas et fait ainsi connaissance avec les objets fractaux :
![]() On pourra
télécharger ici, un énoncé au format Word (x3-1.doc), un corrigé Maple (x3-1.mws)
et une image (x3-1.jpg), le tout dans x3-1.zip.
On pourra
télécharger ici, un énoncé au format Word (x3-1.doc), un corrigé Maple (x3-1.mws)
et une image (x3-1.jpg), le tout dans x3-1.zip.
Bien entendu, les possibilités de Maple (vitesse de calcul, encombrement
mémoire) ne permettent pas une définition très poussée de l'image mais le
résultat est néanmoins suffisant pour appréhender le phénomène.
![]() Le célèbre
automate cellulaire du mathématicien J. Conway fournit un bel exemple,
simple mais didactique, de programmation Maple.
Le célèbre
automate cellulaire du mathématicien J. Conway fournit un bel exemple,
simple mais didactique, de programmation Maple.
![]() Dans un
premier temps, on met en place une programmation simpliste où l'on parcourt
toutes les cases d'un domaine prédéfini et pour le quel on ne s'occupe pas des
effets de bord.
Dans un
premier temps, on met en place une programmation simpliste où l'on parcourt
toutes les cases d'un domaine prédéfini et pour le quel on ne s'occupe pas des
effets de bord.
![]() On améliore
ensuite le programme en profitant des propriétés du type table de Maple,
de façon à ce que le domaine affiché s'agrandisse ou rapetisse en fonction de
l'évolution de la population.
On améliore
ensuite le programme en profitant des propriétés du type table de Maple,
de façon à ce que le domaine affiché s'agrandisse ou rapetisse en fonction de
l'évolution de la population.
Autre subtilité, toujours obtenue grâce aux propriétés des objets de type table,
on ne parcourt que la partie du domaine contenant les individus vivants et
leurs proches voisins.
![]() Une troisième
version du programme inclut une gestion (simpliste) d'un fichier de
populations.
Une troisième
version du programme inclut une gestion (simpliste) d'un fichier de
populations.
![]() On trouvera
ici un énoncé du TP au format Word (jeuvie.doc), quelques exemples de
populations intéressantes (viegr.doc) issues de l'immense bestiaire créé
au fil des ans (par les professionnels, les amateurs et ... les fan-clubs ! ),
et les trois programmes Maple (jeuvie1.mws, jeuvie2.mws, jeuvie3.mws),
le tout dans jeuvie.zip.
On trouvera
ici un énoncé du TP au format Word (jeuvie.doc), quelques exemples de
populations intéressantes (viegr.doc) issues de l'immense bestiaire créé
au fil des ans (par les professionnels, les amateurs et ... les fan-clubs ! ),
et les trois programmes Maple (jeuvie1.mws, jeuvie2.mws, jeuvie3.mws),
le tout dans jeuvie.zip.
![]() On pourra
consulter à propos du jeu de la vie, l'excellent article de Frédéric Neuville
dans SVM n°13 et surtout télécharger le superbe shareware http://psoup.math.wisc.edu/Life32.html
(sans comparaison évidemment, avec ce qu'on obtient en Maple !).
On pourra
consulter à propos du jeu de la vie, l'excellent article de Frédéric Neuville
dans SVM n°13 et surtout télécharger le superbe shareware http://psoup.math.wisc.edu/Life32.html
(sans comparaison évidemment, avec ce qu'on obtient en Maple !).
![]() Bifurcation : un résultat édifiant à propos des suites
récurrentes un+1 = f(un)
Bifurcation : un résultat édifiant à propos des suites
récurrentes un+1 = f(un)
![]() Il s'agit du
schéma de Feigenbaum bien connu, tout à fait visualisable avec Maple.
Il s'agit du
schéma de Feigenbaum bien connu, tout à fait visualisable avec Maple.
On considère la suite récurrente un+1 = f(un)
avec f(x) = l x(1-x)
(0<l<4) dont les valeurs
d'adhérences se répartissent suivant l
de l'étonnante façon que l'on sait.
Pour le visualiser, on porte en abscisse les valeurs de l puis, pour chaque valeur de l
(de dl en dl ), on reporte en ordonnée les valeurs de un
, pour n entre 20 et 50 par exemple, valeurs déjà assez importantes pour
que les diverses valeurs d'adhérence soient approchées d'assez près :
![]() On trouvera
ici un énoncé de TP au format Word (bifurc.doc), un corrigé Maple (bifurc.mws),
le tout dans bifurc.zip.
On trouvera
ici un énoncé de TP au format Word (bifurc.doc), un corrigé Maple (bifurc.mws),
le tout dans bifurc.zip.
![]() Je ne peux
que signaler, à propos de cet exemple (et de celui du bassin d'attraction plus
haut), l'excellent cours sur les objets fractaux et les systèmes
dynamiques, entièrement ‘illustré’ en Maple, dû à Alain Schauber et dont
les programmes en Maple sont accessibles à http://www.oci.uzh.ch/mirror/maple/frame03.htm
.
Je ne peux
que signaler, à propos de cet exemple (et de celui du bassin d'attraction plus
haut), l'excellent cours sur les objets fractaux et les systèmes
dynamiques, entièrement ‘illustré’ en Maple, dû à Alain Schauber et dont
les programmes en Maple sont accessibles à http://www.oci.uzh.ch/mirror/maple/frame03.htm
.
![]() Un excellent
sujet qui débute dans l'esprit du calcul formel, avec de belles manipulations
de polynômes et qui se poursuit par des approximations numériques minutieuses
demandant réflexion et finesse. Ce TP illustre bien les différentes
utilisations possibles de Maple.
Un excellent
sujet qui débute dans l'esprit du calcul formel, avec de belles manipulations
de polynômes et qui se poursuit par des approximations numériques minutieuses
demandant réflexion et finesse. Ce TP illustre bien les différentes
utilisations possibles de Maple.
![]() On peut (si
l’on y est autorisé) télécharger ce TP depuis le serveur ftp ftp://ftp.ac-dijon.fr/carnot1/maths/TP-Maple/,
géré par Michel Quercia,
professeur au lycée Carnot de Dijon.
On peut (si
l’on y est autorisé) télécharger ce TP depuis le serveur ftp ftp://ftp.ac-dijon.fr/carnot1/maths/TP-Maple/,
géré par Michel Quercia,
professeur au lycée Carnot de Dijon.
![]() A la limite
(extérieure !) des programmes des Classes Préparatoires mais tout à fait
abordables par leurs élèves, moyennant quelques définitions supplémentaires et
résultats (admis).
A la limite
(extérieure !) des programmes des Classes Préparatoires mais tout à fait
abordables par leurs élèves, moyennant quelques définitions supplémentaires et
résultats (admis).
![]() Un moyen
quelque peu ludique de manipuler l'arsenal de base d'analyse de Maple :
dérivation, intégration, équations et systèmes différentiels (avec résolutions
formelles et numériques), ...
Un moyen
quelque peu ludique de manipuler l'arsenal de base d'analyse de Maple :
dérivation, intégration, équations et systèmes différentiels (avec résolutions
formelles et numériques), ...
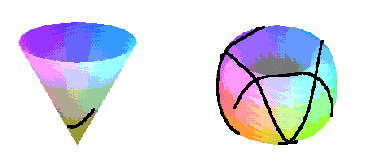
![]() On trouvera
tout ceci dans geodesiq.zip.
On trouvera
tout ceci dans geodesiq.zip.
![]() Droite des moindres carrés pour un nuage fini de
points
Droite des moindres carrés pour un nuage fini de
points
![]() Sujet hyper-classique dont on trouvera deux
approches :
Sujet hyper-classique dont on trouvera deux
approches :
v Réduction de la forme quadratique associée au nuage de points et de sa matrice puis détermination de la plus petite des valeurs propres et affichage des directions propres associées (dans un repère centré au centre de gravité préalablement calculé) :

v Recherche de minimas par annulation de dérivées partielles.
![]() On trouvera un corrigé Maple dans MoindrCa.zip .
On trouvera un corrigé Maple dans MoindrCa.zip .
![]() Il
s’agit d’abord de l’étude de la transformation dite de Conway, qui à un
mot
Il
s’agit d’abord de l’étude de la transformation dite de Conway, qui à un
mot ![]() d’un alphabet
A
contenant l’ensemble des entiers, associe le mot
d’un alphabet
A
contenant l’ensemble des entiers, associe le mot ![]() .
.
(m1 , m2 , .. , mr sont des entiers non nuls et si m
est un entier non nul et a un élément de
A
, am représente le mot aaa .. a où a apparaît
m fois)
Conway a démontré que la longueur du nième mot obtenu par
application itérée n fois du procédé, suit une loi du type C x
( L )n où C
dépend (assez peu) du mot initial et où
L (constante de Conway) est la plus grande
racine réelle du polynôme suivant (!) :
x71-x69-2x68-x67+2x66+2x65+x64-x63-x62-x61-x60-x59+2x58+5x57+3x56-2x55-10x54
-3x53-2x52+6x51+6x50+x49+9x48-3x47-7x46-8x45-8x44+10x43+6x42+8x41-5x40
-12x39+7x38-7x37+7x36+x35-3x34+10x33+x32-6x31-2x30-10x29-3x28+2x27+9x26
-3x25+14x24-8x23-7x21+9x20+3x19-4x18-10x17-7x16+12x15+7x14+2x13-12x12-4x11
-2x10+5x9+x7-7x6+7x5-4x4+12x3-6x2+3x-6
![]() Dans le même sujet, on étudie quelques suites
(très !) récurrentes de Conway et de Conway-Hofstadter aux évolutions et
comportements à la limite assez étonnants.
Dans le même sujet, on étudie quelques suites
(très !) récurrentes de Conway et de Conway-Hofstadter aux évolutions et
comportements à la limite assez étonnants.
![]() Sujet
et corrigé Maple dans SuitExot.zip .
Sujet
et corrigé Maple dans SuitExot.zip .
![]() Un
nombre de Carmichael est un entier
N non premier et vérifiant
le petit théorème de Fermat, à savoir que pour tout entier a
non multiple de N , aN-1 est congru à 1
modulo N .
Un
nombre de Carmichael est un entier
N non premier et vérifiant
le petit théorème de Fermat, à savoir que pour tout entier a
non multiple de N , aN-1 est congru à 1
modulo N .
![]() Il s’agit ici, d’utiliser différentes et
subtiles caractérisations pour rechercher de très grands nombres de Carmichael.
Il s’agit ici, d’utiliser différentes et
subtiles caractérisations pour rechercher de très grands nombres de Carmichael.
![]() Ce TP est adapté d’une étude du livre « Maple,
son bon usage en mathématiques » de Philippe Dumas et Xavier Gourdon
[Springer, 1997] (pages 127 et 373). Enoncé et corrigé sont réunis dans Carmich.zip .
Ce TP est adapté d’une étude du livre « Maple,
son bon usage en mathématiques » de Philippe Dumas et Xavier Gourdon
[Springer, 1997] (pages 127 et 373). Enoncé et corrigé sont réunis dans Carmich.zip .
![]() Un bel
exemple de calcul formel, avec de gros calculs dans l'extension de corps Q[j,Ö 3] et dans l'espace des polynômes
construits sur ce corps. La puissance de Maple bien employé est ici assez
spectaculaire.
Un bel
exemple de calcul formel, avec de gros calculs dans l'extension de corps Q[j,Ö 3] et dans l'espace des polynômes
construits sur ce corps. La puissance de Maple bien employé est ici assez
spectaculaire.
![]() On trouvera
l'énoncé et le corrigé de ce TP dans le livre "15 thèmes
mathématiques" de Paul Donato, publié en 1997 chez Diderot.
On trouvera
l'énoncé et le corrigé de ce TP dans le livre "15 thèmes
mathématiques" de Paul Donato, publié en 1997 chez Diderot.
![]() Polynômes à coefficients dans {0,1}
Polynômes à coefficients dans {0,1}
![]() On étudie la
densité (locale) des racines complexes des polynômes dont les coefficients sont
des 0 ou des 1 , dans le domaine du plan complexe défini par |z| £ 1 et |z| / ( 1 - |z| ) £ | 2 - z | / | 1 - z | . Le résultat est
surprenant et tout à fait abordable avec Maple.
On étudie la
densité (locale) des racines complexes des polynômes dont les coefficients sont
des 0 ou des 1 , dans le domaine du plan complexe défini par |z| £ 1 et |z| / ( 1 - |z| ) £ | 2 - z | / | 1 - z | . Le résultat est
surprenant et tout à fait abordable avec Maple.
![]() On trouvera
l'énoncé et le corrigé de ce TP dans le livre "Mathématiques et
Informatique ; quatorze problèmes corrigés pour l'enseignement supérieur"
de François Morain et Jean-Louis Nicolas, publié en 1995 chez Vuibert.
On trouvera
l'énoncé et le corrigé de ce TP dans le livre "Mathématiques et
Informatique ; quatorze problèmes corrigés pour l'enseignement supérieur"
de François Morain et Jean-Louis Nicolas, publié en 1995 chez Vuibert.
![]() Pavages apériodiques de Penrose
Pavages apériodiques de Penrose
![]() Un très bel
exemple de pavage apériodique du plan à l'aide de deux types de triangles.
Un très bel
exemple de pavage apériodique du plan à l'aide de deux types de triangles.
![]() En voici une
approche pragmatique quant à sa construction, développée pour Caml par Philippe Saunois, professeur en
Sup au lycée Lamartinière à Lyon et dont je donne une version Male avec Penrose.zip.
En voici une
approche pragmatique quant à sa construction, développée pour Caml par Philippe Saunois, professeur en
Sup au lycée Lamartinière à Lyon et dont je donne une version Male avec Penrose.zip.

![]() Un thème
abordé en exercice dans le livre de Gomez, Salvy et Zimmermann : "Calcul
formel : mode d'emploi - Exemples en Maple" et dont le
corrigé se trouve donc à http://www.loria.fr/~zimmerma/maple/
Un thème
abordé en exercice dans le livre de Gomez, Salvy et Zimmermann : "Calcul
formel : mode d'emploi - Exemples en Maple" et dont le
corrigé se trouve donc à http://www.loria.fr/~zimmerma/maple/
![]() Il s'agit
d'une représentation originale dans le plan des entiers premiers où l'on met en
évidence des alignements des plus mystérieux (pas tant que ça en fait, mais
spectaculaires !). Un bel exemple de l'utilisation des fonctions arithmétiques
simples de Maple.
Il s'agit
d'une représentation originale dans le plan des entiers premiers où l'on met en
évidence des alignements des plus mystérieux (pas tant que ça en fait, mais
spectaculaires !). Un bel exemple de l'utilisation des fonctions arithmétiques
simples de Maple.



![]() Ce
sujet est tiré d’un article du numéro spécial de décembre 2000 « Les
infinis » de « Pour la
science » . Il s’agit de « L’infini est-il
nécessaire ? », de Patrick Dehornoy, article qu’il faut avoir lu
avant d’aborder le sujet.
Ce
sujet est tiré d’un article du numéro spécial de décembre 2000 « Les
infinis » de « Pour la
science » . Il s’agit de « L’infini est-il
nécessaire ? », de Patrick Dehornoy, article qu’il faut avoir lu
avant d’aborder le sujet.
![]() On construit là des suites d’entiers d’une
croissance incroyablement rapide (voir également le sujet suivant) par simple
bricolage de la décomposition en facteurs premiers du terme initial. C’est
cette transformation qui est très intéressante à programmer avec Maple.
On construit là des suites d’entiers d’une
croissance incroyablement rapide (voir également le sujet suivant) par simple
bricolage de la décomposition en facteurs premiers du terme initial. C’est
cette transformation qui est très intéressante à programmer avec Maple.
![]() Sujet et corrigé Maple dans Goodstein.zip .
Sujet et corrigé Maple dans Goodstein.zip .
![]() Tables de Laver et fonction d’Ackermann
Tables de Laver et fonction d’Ackermann
![]() Là
encore, ce sujet est tiré d’un article du numéro spécial de décembre 2000 « Les
infinis » de « Pour la
science » . Il s’agit de « L’infini est un
révélateur », toujours de Patrick Dehornoy, article qu’il faut lire
avant d’aborder le sujet. On y apprend que la croissance très rapide vers
l’infini de suites de certaines périodes apparaissant dans ces tables est liée
à l’existence d’ensembles « extrêmement grands », dits ensembles
hyperinfinis.
Là
encore, ce sujet est tiré d’un article du numéro spécial de décembre 2000 « Les
infinis » de « Pour la
science » . Il s’agit de « L’infini est un
révélateur », toujours de Patrick Dehornoy, article qu’il faut lire
avant d’aborder le sujet. On y apprend que la croissance très rapide vers
l’infini de suites de certaines périodes apparaissant dans ces tables est liée
à l’existence d’ensembles « extrêmement grands », dits ensembles
hyperinfinis.
![]() Une croissance aussi importante est approchée
par la fonction d’Ackermann, elle même tellement croissante qu’elle
n’est pas récursive-primitive (voir le sujet précédent et mes pages sur
les Machines de Turing).
Une croissance aussi importante est approchée
par la fonction d’Ackermann, elle même tellement croissante qu’elle
n’est pas récursive-primitive (voir le sujet précédent et mes pages sur
les Machines de Turing).
![]() Sujet et corrigé Maple dans Laver.zip .
Sujet et corrigé Maple dans Laver.zip .
![]() Un
entier de Hamming est un entier qui n’est pas divisible par d’autres
entiers premiers que 2 , 3 ou 5 .
Un
entier de Hamming est un entier qui n’est pas divisible par d’autres
entiers premiers que 2 , 3 ou 5 .
![]() On met alors en place des algorithmes du plus
simple au plus sophistiqué pour rechercher des entiers de Hamming les plus
« grands » possible. Les derniers algorithmes, extrêmement subtils,
sont tirés d’un article de Michel
Quercia de 1999.
On met alors en place des algorithmes du plus
simple au plus sophistiqué pour rechercher des entiers de Hamming les plus
« grands » possible. Les derniers algorithmes, extrêmement subtils,
sont tirés d’un article de Michel
Quercia de 1999.
![]() On trouvera l’article de Quercia, le sujet et
le corrigé Maple dans Hamming.zip .
On trouvera l’article de Quercia, le sujet et
le corrigé Maple dans Hamming.zip .
![]()
A SUIVRE !
![]()